|
一種精確測定超短基線真方位角的方法1 引言 工程測繪中,基線方向常用高斯投影面坐標方位角來表示,在特定情況下則需要測定基線的真方位角,如地質與地球物理勘探、 航空、 航海、 炮兵射擊雷達定向等。 所謂真方向角,即某點指向北極的方向線叫真北方向線,也叫真子午線,從該點的真北方向線起,依順時針方向到目標方向線間的水平夾角,叫該點的真方位角勺。 確定一條基線真方位角的方法,通常有陀螺全站儀法、 高斯投影改正法。 由控制測量可知,求解基線坐標方位角,兩端已知點間距越長,解算越精確,反之,邊長越短,其坐標方位角精確求解越困難。 同樣,求解真方位角亦是如此,例如在針對飛機慣導系統進行檢校與標定時,其長度僅幾十米,若要精確解算其真方位角,是極其困難的,因為在短距離中,GNSS觀測天線相位中心偏差、儀器校準誤差、觀測星歷等因素對其方位計算影響較大。 在超短基線定位領域,有學者已經做了許多相關研究工作,如:李瑜等以3種不同長度的基線,對比分析了PPE軟件24h數據的處理精度同;王德剛等著重分析了超短基線定位的誤差來源⑺;楊貴海等從測距誤差、測深誤差著手,提高了測量設備的定位精度劇。 類似上述的研究不少,但前人或從軟件測試角度,或從仿真技術入手,主要探討的是點位精度,而非真方位角。此外,傳統高斯投影法在求解真方位角時,需將大地坐標投影至高斯平面,再反算其坐標方位角、 子午線收斂角、 方向改化,方可獲得真方位角,該過程繁瑣、解算易出偏差、 實用性不強。 為精確、 便捷求解超短基線真方位角,本研究基于站心地平坐標系的基礎理論,結合某飛機慣導檢驗項目,分析、 探討了站心地平坐標系在飛機慣導檢驗測試中求解超短基線真方位角的實踐運用。 通過與傳統高斯投影改正法的對比,該方法在精度上無損失,且求解便捷,提高了實用性。 2站心地平坐標系計算模型站心地平坐標系以測站P為原點,以P點的法線為Z軸,取大地天頂距方向為正方向。 地表上,以子午線方向為x軸,y軸與x軸、 z軸正交,它與空間直角坐標系所屬的兩種坐標系的坐標原點及3個坐標軸的指向均不同,存在著平移旋轉的關系。 站心地平坐標系一般用于深空大地測量研究,由于真方位是確定單個點位到另一點位的方位,因此本文利用站心地平坐標系的定義對兩點間的方位進行求解。 基于該計算理論,可推知用于求解基線邊真方位角的計算模型。
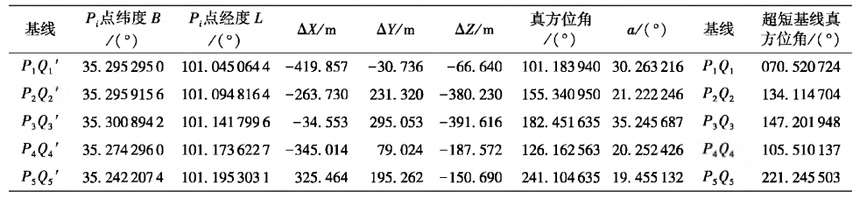
圖1空間直角坐標系與站心地平坐標系示意圖 3計算實例 3. 1基于站心地平坐標系的計算 基于上述站心地平坐標系計算模型,以某機場超短基線真方位角作為工程背景,本文在另一測區進行實地布點與觀測,進行了前期案例的解算試驗。 工程待求基線長50 m,要求觀測精度達0.005。 (18〃)。 本文實際布設邊長30-40 m,共布設12條基線,并進行了實地GNSS觀測,觀測與真方位角的解算結果見表1。 首先利用GNSS觀測,測定化點的大地坐標(B"),計算每條基線化Q'空間大地宜角坐標,獲取化與G'兩點的
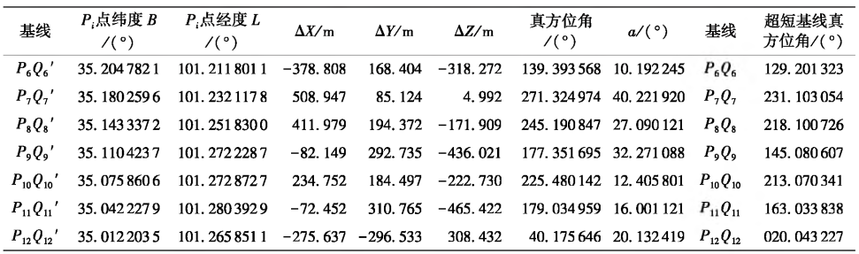
表1站心地平坐標系真方位角觀測與解算結果
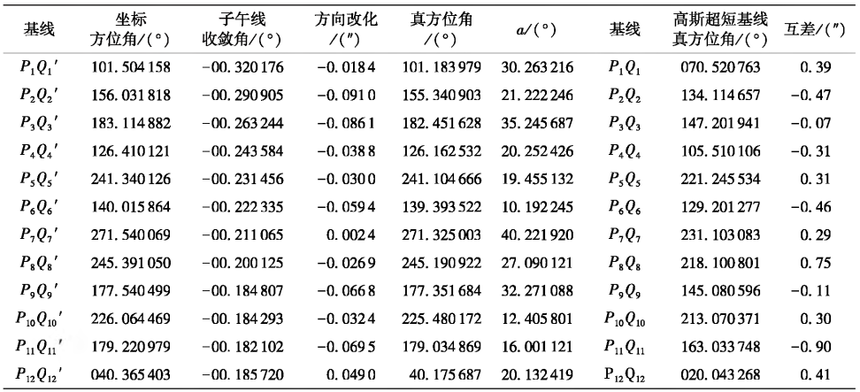
3.2基于高斯投影法的驗證 關于上述基于站心地平坐標系求解超短基線真方位角的正確性,本文運用傳統高斯投影法進行了驗證。 高斯投影法即將橢球面上兩點的大地坐標投影至高斯平面,獲取該基線的坐標方位角,將其經過子午線收斂角與方向改化后,可獲得該基線的真方位角。 本驗證實例采用WGS 84橢球,計算子午線收斂角時的中央子午線經度為102。 ,計算結果見表2,同樣,先計算每條長基線邊匕的真方位角,其投影后的坐標方位角與化點處的子午線收斂角,以及橢球面圓弧投影至平面后產生的方向改化三者之和即為化Q/的真方位角,針對該繁瑣的討算過程,本文借助VC++6.0平臺,編制了該過程的求解程序,最后通過«值可宜接將其真方位角引至超短揺PQ。
表2高斯投影法驗證結果 4 結束語 站心地平坐標系通常用于深空大地測量,但鑒于其坐標系原點設于測站中心這一顯著特征,有助于引出該基線另一端點在該站心地平坐標系中的坐標,從而快速解得基線真方位角。 從計算模型看,該方法與高斯投影法最顯著的不同,是它規避了中間求解子午線收斂角與方向改化的繁瑣環節。 而本文方法,雖需求解基線端點的空間宜角坐標,但在實踐中,其GNSS靜態解算成果已含有該基線向量,即公式(1)中求得兩點在空間宜角坐標系下的坐標差,它為整體真方位角的求解節省了巨大的工作量,可宜接利用公式(5)與真方位角計算公式,解算基線真方位角。 從計算環節看,高斯投影法計算繁瑣、 實用性弱,本文所用方法簡單、 快捷、 實用性強;精度上,兩種方法互差均控制在1"以內,平均差值0. 397〃,其真方位角結果完全滿足0. 005。 ( 18〃 )的精度要求。 因此,基于站心地平坐標系的超短基線真方位角計算方法較傳統計算方法優勢明顯,可用于同類項目的實踐生產與研究。 同時,也應看到,上述均是在內業解算方案上的探討,而所有測量項目,其精度主要取決于外場觀測,本研究為確保觀測精度,所有觀測點均使用了強制觀測墩,這一方案不但大大提高了測量成本,也使得測量效率變得極為低下。 因此,在不使用強制觀測墩的情況下,如何高效、 確保觀測精度,是今后需要關注的方向。 參考文獻 [1]施一民.現代大地控制測量[M].北京:測繪出版社,2003. [2] 王解先,劉慧芹,唐立軍.不同站心地平坐標系下的坐標歸算[J].工程勘察,2005(5) :58-60. |